In all fairness: Engineering Fairness in Modern Machine Learning Algorithms

I was a young bright eyed MS student at NeurIPS 2017 taking it all in - CNNs were still the rage, LeCun was still a celebrity and the air was filled with possibilities of these deep neural networks addressing problems that were thought to be pretty difficult up until now (unlike today where everything is some version of LLM applied to x-problem sigh). Engineers often focus on making a problem work and often overlook a crucial factor in engineering - it has to interact with people in the real world. It was at this conference that I had the good fortune of listening to Kate Crawford’s keynote on the inherent bias in machine learning algorithms. I found it especially interesting since many of the systems even today display (un-)intentional bias.

Like many good ideas that pop into my mind, I had pushed it in the “sounds fun, may attempt something on it later” shelf in my mind closet. It stayed there until the first year of my PhD when my advisor asked me to look into this problem.

The Problem Setup

I considered a supervised learning setup in this problem. This meant that I assumed a dataset $\mathcal{D}$ consisting of a 3-tuple $(\mathbf{x}_i, y_i, s_i)$. The first two are pretty standard - a n-dimensional data point and the associated label. The third component is interesting. In fairness literature this is is called the sensitive attribute.

Imagine you’re a banker whose main job is to either approve or deny a loan to an individual. You may look at the person’s age, gender, income, race, education and based on the available data (in your Excel sheet) you decide if this person is worth the risk. Now, as a human you can let your bias creep in the process but the flip side is that you will be held accountable in case the denied person decides to sue you.

On the other hand, if you offload the task to a machine with “advanced” AI algorithms, no one can be held accountable since the outcome is determined by the machine based on countless comparisons from previous cases. You can simply shrug and walk away. There’s a catch however - the “AI” that you used may have been trained on a dataset that encoded some sort of biases in the training set itself! For example, individuals belonging to certain age or gender were labeled as denied more frequently than others. This particular feature in data is called a sensitive feature or sensitive attribute since it biases a machine learning algorithm’s output on some features which inherently must be ignored by an impartial human.

When I read through the literature on this topic, something bothered me for days. One day, it clicked. The problem with defining this $s_i$ beforehand and optimizing a machine learning algorithm to remove dependence on $s_i$ is like telling a child to close it’s ears when it hears a particular phrase. However, children are intelligent and can often guess what you’re gonna say based on context and past data. Similarly, machine learning algorithms will learn associations between features and still secretly bias their decisions on the sensitive feature. Reading more and more into this, I had two insights:

1. Not all features (including $s_i$) contribute equally to the model’s output.
2. Removing dependence on $s_i$ for decision making is not foolproof - the model may use proxy sensitive features to make predicitions.

From insights to algorithmic components

The first insight implies that there exist a subset of features in data that contribute most towards the overall performance of the model. I called this subset a critical feature set.

How do we find such a set? We clearly cannot assume it from examining the data. My solution was to run a pre-processing step on the training set:

• First, I define a metric $\mathcal{M}$ that I measure to evaluate the model’s performance. For different tasks, these can be accuracy, mean squared error or F1 score.

• Partition the training data into $K$ non overlapping folds. Then train the model on $K-1$ fold and evaluate the performance on the remaining fold.

• Run the procedure $N$ times with feature permutation (this prevents the machine learning model from “cheating” by memorization).

At the end of the procedure, I would have built a “feature importance vector” $\mathcal{I}_x$ where $f_i \in \mathcal{I}_x$:

$$ f_i = \Delta - \frac{1}{N}\sum_{i}^N \delta_i $$

Here $\Delta$ is the metric value when no features are permuted and $\delta_i$ is the metric value when the $i^{th}$ permutation is applied to the data.

The second insight implied that the input sensitive variable $s_i$ may have correlations with other features within the data. Thus, as a second pre-processing step, I estimate $\Sigma$ by fitting a maximum likelihood estimator on the training data.

Testing the insights on real data

To evaluate these insights on real world datasets, I selected two representative datasets. The first one called ADULT is a collection of people described by various features like age, race, gender, education etc. The task is to determine if they are good candidate for a loan. The second one is the famous COMPAS dataset that accompanied the story about how a machine learning decision system was more likely to re-incarcerate African-Americans than white Americans. The sensitive feature in ADULT dataset is the person’s gender while in COMPAS it’s race of the individual.

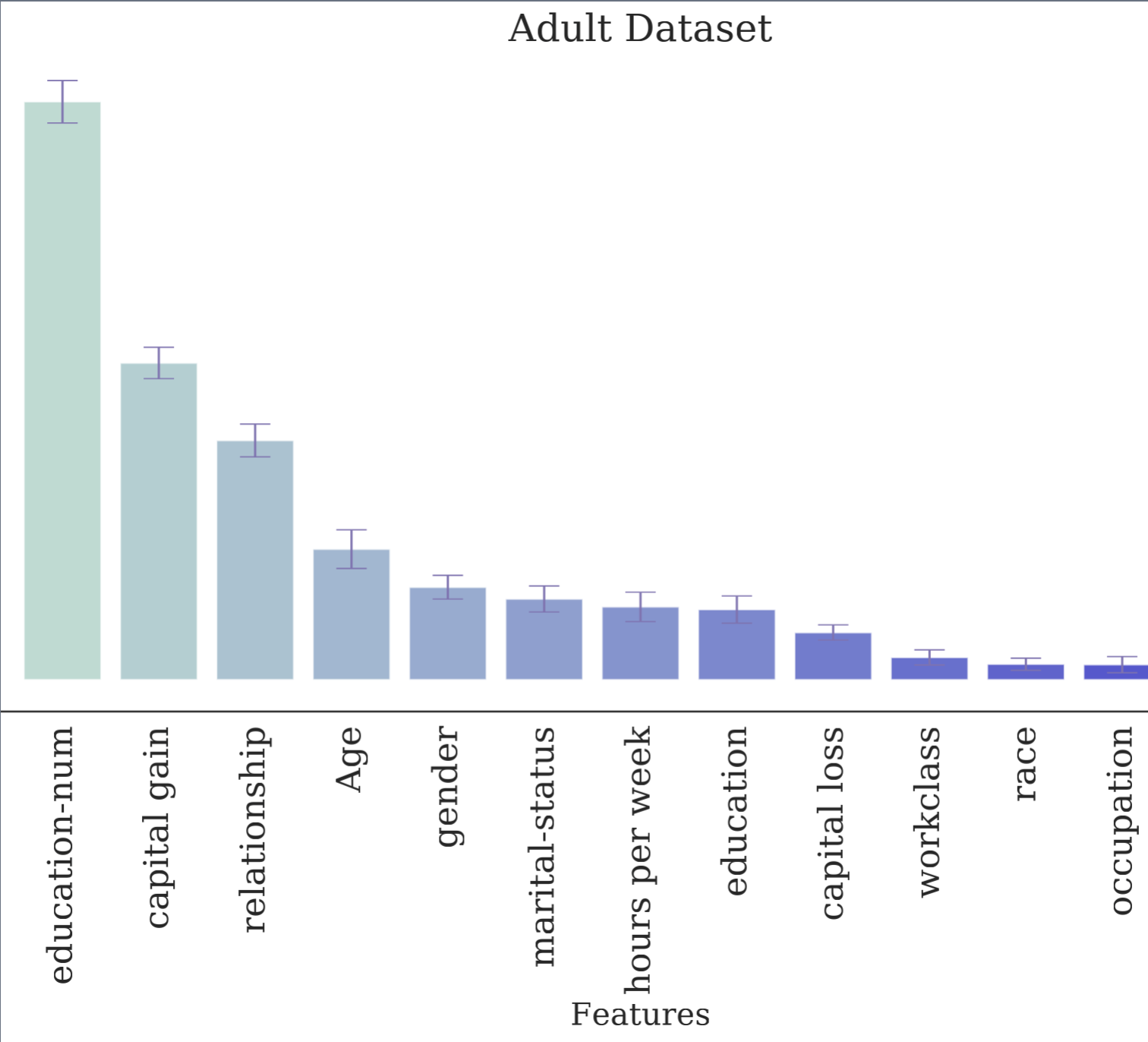
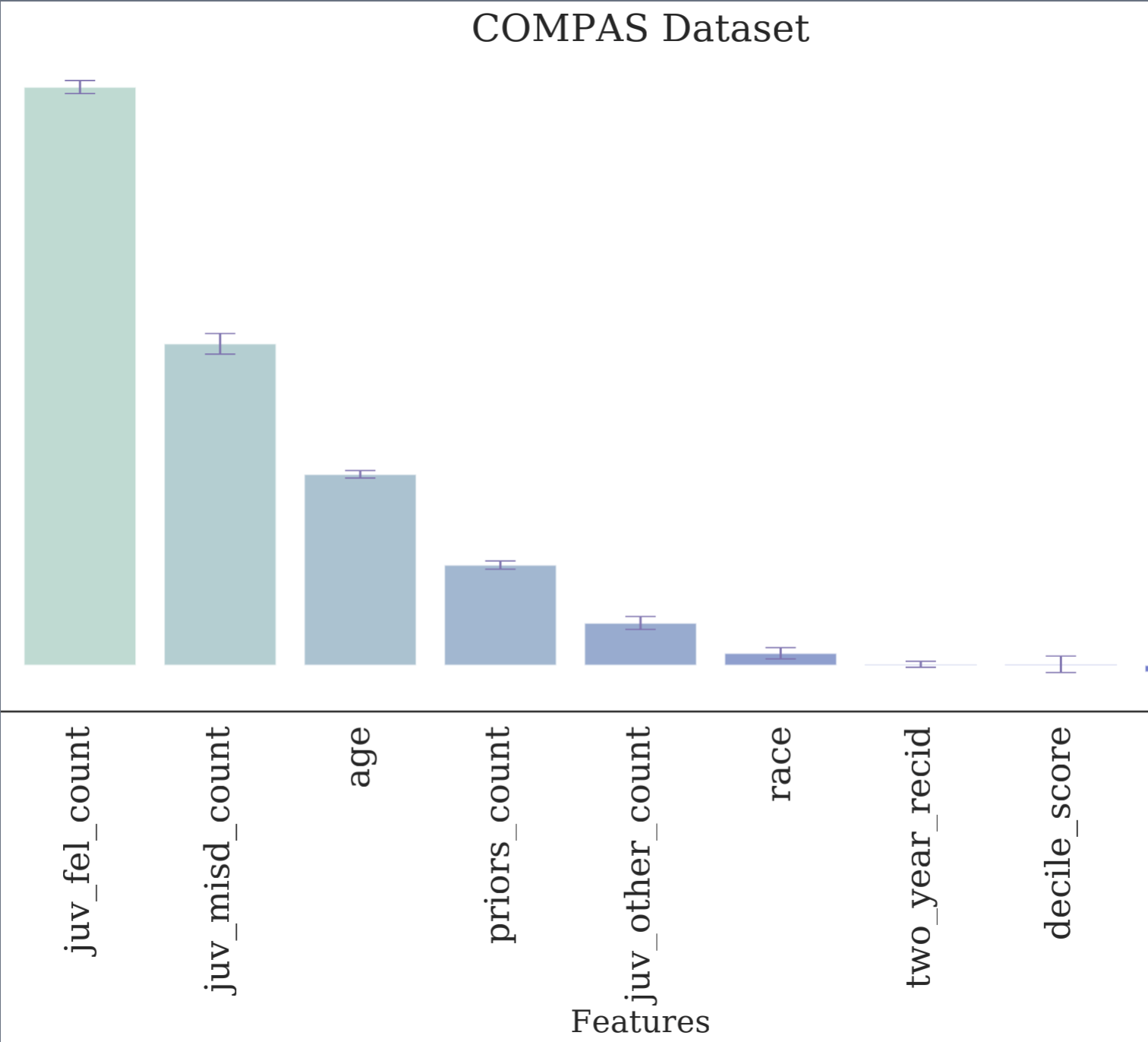
The outcome of computing feature importance is very interesting. You can see for yourself that neither gender nor race have a significant effect on the prediction of the machine learning systems on their own. Thus, if they are providing biased results it must be because of these features being correlated with more predicitve ones.

Measures of Fairness

For a supervised learning paradigm, we define three distinct variables. $\hat{Y}$ is the predicted variable by a supervised learning algorithm, $\mathcal{Y}$ is the ground truth label and $\mathcal{S}$ is the sensitive feature of the data point.

Now, if we do have access to the ground truth labels, we can evaluate the fairness by conditioning the outcome on $\mathcal{Y}$. Some criteria that fall in this category are Equal Odds (where $D = -1 \perp \mathcal{S} | \mathcal{Y} = 1$ and $D = 1 \perp \mathcal{S} | \mathcal{Y}=1$)¹, and Equal Opportunity (where $D = 1 \perp \mathcal{S} | Y=1$)²³. A defining characteristic of these metrics is that they can be interpreted as a score function $\mathcal{L}: \mathcal{X} \times \mathcal{S} \times \mathcal{Y} \rightarrow \mathbb{R}$. For instance, the Equal Opportunity metric can be expressed as

$$ \mathcal{L}(\mathcal{X}, \mathcal{S}, \mathcal{Y})= \mathbb{E}[|l^{+}_a(f(\mathbf{x}_i, y_i)) - l^{+}_b(f(\mathbf{x}_i), y_i))] $$

and a corresponding score function for Equality of True Negative Rates can be written as

$$ \mathcal{L}(\mathcal{X}, \mathcal{Y}, \mathcal{S}) = \mathbb{E}[|l^{-}_a(f(\mathbf{x}_i), y_i) - l^{-}_b(f(\mathbf{x}_i), y_i)|] $$

Here, $l^{\pm}_{g}$ is the per sample loss for any learning algorithm $f$ on either positively or negatively labeled points belonging to a sensitive group $g$.

It is nice and easy to have metrics defined in terms of ground truth. However, there are cases when we can only observe bias in a system by observing the predicted outcome. For example, a facial scanning system that predicts if you’re a criminal or not generally doesn’t provide access to the training data of mugshots it was trained on. Hence, we need metrics that can evaluate fairness based on predicted outcomes $\hat{Y}$. Some examples of metrics belonging to this class are Equality of Negative Predictive Value (def: $Y = -1 \perp \mathcal{S} | \hat{Y}=-1$) and Equality of Positive Predictive Value (def:$\mathcal{Y} = 1 \perp \mathcal{S} | \hat{Y}=1$). In other words, if a outcome was negative then it should correspond to a negative groundtruth label irrespective of the value of $S$.

Modeling constraints within machine learning algorithms

Now that we know what metrics are used to define fairness, we are in a good position to try and train a machine learning algorithm to respect these metrics for making fair-er predictions.

Let’s take the equal oppportunity metric as an example. The metric is defined as $P(\hat{Y}=1 | S=a, Y=1) - P(\hat{Y}=1 | S=b, Y=1) \leq \epsilon$. Here $\hat{Y}$ is the predicted value given an input datapoint i.e. $\hat{Y} = f(\mathbf{x})$. Here $\epsilon$ is the degree of unfairness we’re willing to tolerate in the system. Prior to my work⁴ it was standard to set $\epsilon = 0$.

However, I realized that we cannot make perfectly fair systems without damaging the performance of the model irreparably (and if we could achieve perfect fairness then the world would somehow become utopia). Hence, I made a simple modification to allow a user to determine how much fairness they want in their system. Hence, my formulation accepts $\epsilon = f_{tol}$ where $f_{tol}$ is user provided.

Let’s revisit the loss $L(\mathcal{X}, \mathcal{Y}, S)$ defined above. The general idea in introducing fairness into the system is to somehow integrate the constraint $L(\mathcal{X}, \mathcal{Y}, S) \leq \epsilon$ where $\epsilon$ is either user defined or zero.

Linear models of machine learning model $f(\mathbf{x})= \langle \mathbf{w}, \phi(\mathbf{x})\rangle$ where $\phi(\mathbf{x})$ is some feature mapping and $\langle x, y\rangle = x^Ty$ a.k.a inner product. The weight vector $\mathbf{w}$ is essentially a separating hyperplane that can classify a data point into distinct categories. The simplest case of feature mapping is $\phi(\mathbf{x}) = \mathbf{x}$. There’s a cool “trick” in machine learning that allows us to compute a high dimensional mapping from a given dataset. Why high dimensional? Because it may so happen that our dataset is non separable by $\mathbf{w}$ in the given number of dimensions. However, in some high dimensional space, it may be linearly separable. This “trick” is the kernel-trick that allows us to compute $\langle \phi(\mathbf{x}), \phi(\mathbf{x’})\rangle$ by simply computing the kernel matrix $K(\mathbf{x}, \mathbf{x’})$ for $\mathbf{x}, \mathbf{x’} \in \mathcal{X}$. The advantage of defining a kernel like this is that we don’t really need to worry about finding a “good enough” feature mapping. A famous example of kernel is the RBF Kernel $K(\mathbf{x}, \mathbf{x}’) = e^{-\gamma ||\mathbf{x} - \mathbf{x’}||_2}$.

One of the best linear models to use in supervised learning is the Support Vector Machine (SVM). The unconstrained objective function can be written as:

$$ \min_{\mathbf{w}} \sum_{i=1}^n l(f(\mathbf{x}), y) + \lambda ||\mathbf{w}||_2 $$

Where $\lambda ||\mathbf{w}||_2$ is the regularization constraint on the weight vector so that it’s constrained within a ball of radius $\lambda$. But how do we integrate a fairness constraint like Equal Opportunity in training a linear model? We know we need to constrain the weight vector $\mathbf{w}$ to disregard the sensitive variable somehow. Donini et al.² propose a constraint of the form $\langle \mathbf{w}, \mathbf{u} \rangle \leq \epsilon$ where $\mathbf{u}$ is the centroid of positively labeled points belonging to a particular sensitive group. So if $\mathcal{S} = {a, b}$:

$$ \mathbf{u_{g}} = \sum_{j=1}^{n} \frac{\phi(\mathbf{x}_j)}{N^{+}_g} $$

Then to draw a hyperplane that strictly respects the EO metric, we need to have the weight vector orthogonal to $\mathbf{u}_a - \mathbf{u}_b$. In other words $\langle\mathbf{w}, \mathbf{u}_a - \mathbf{u}_b\rangle$. So the modification to the SVM objective is:

$$ \min_{\mathbf{w}} \sum_{i=1}^n l(f(\mathbf{x}), y) + \lambda ||\mathbf{w}||_2\ s.t. \langle \mathbf{w}, \mathbf{u}_a - \mathbf{u}_b\rangle = 0 $$

To integrate the user defined fairness tolerane $f_{tol}$ we can adjust this constraint to be $\langle \mathbf{w}, \mathbf{u_a} - \mathbf{u_b}\rangle \leq f_{tol}$.

One can then setup the dual of the constrained optimization problem and solve for the support vector coefficients $\mathbf{\alpha}$ that respect the constraint. The package CONFAIR implements all code for fairness evaluation using SVMs. It supports $f_{tol} = 0$ and $f_{tol} \neq 0$ cases.

How much fairness is enough?

The literature I read at that time suggested we needed absolutely good performance on the given fairness metric. If we step back and look at the law of conservation, it will become apparent that a gain in some quantity must come at the expense of another. In this case the predictive accuracy is the obvious victim. The other victim is more subtle - by increasing fairness on one metric by strict constraints, we may end up being unfair in the opposite direction. For example, by ensuring the positive predictions do not take the sensitive variable into account we may condition the negative prediction on the said sensitive variable.

To measure this I optimized the SVM with $f_{tol} = 0$ and $f_{tol} \neq 0$ and measured the Difference in Equal Opportunity (DEO) along with the NPV of the trained SVM on the test set. This is what I got:

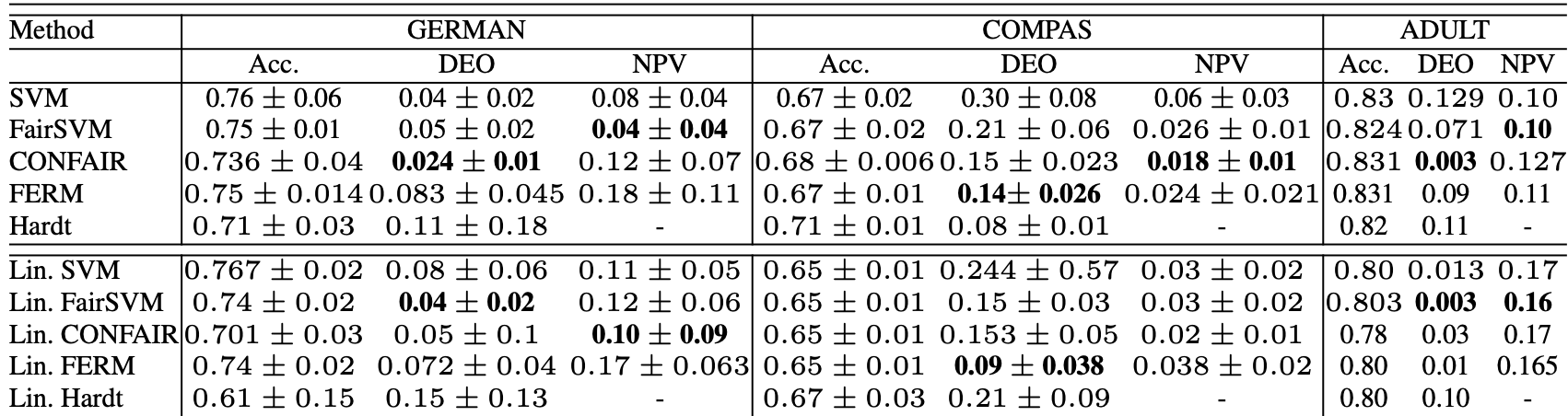
Here FERM is the case when $f_{tol} = 0$ and FairSVM is trained on full feature set with $f_{tol} \neq 0$. You can see that when choosing the right set of features and optimizing less strictly, we can get better performance on both explicit and implicit fairness objectives. I also benchmarked the effect of varying $f_{tol}$ on various cases as well:

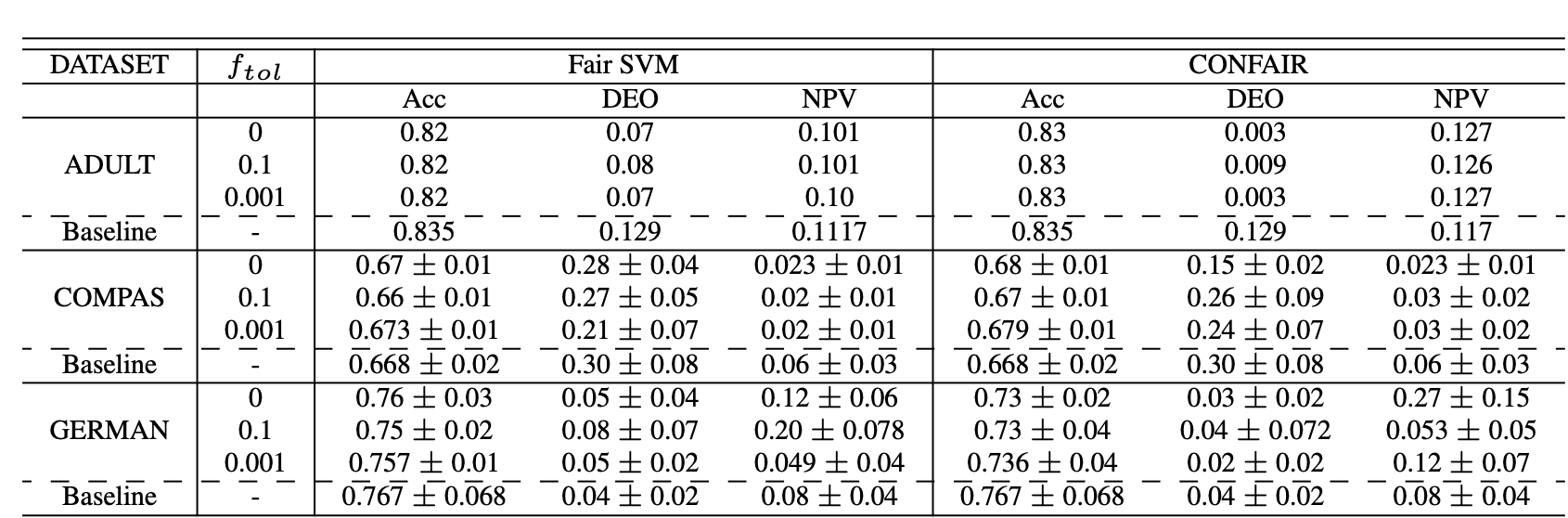
We can see that different values of $f_{tol}$ produce different amounts of fairness in different datasets. Thus, the tolerance is a highly data-dependent hyperparameter and can be chosen depending on the needs of the algorithm designer.

Conclusion

As we enter into an era where AI models are ubiquitous, we need to be especially careful about the inherent bias that these models absorb when trained on biased data created by us. This blog post discusses some ways in which fairness can be included in a given AI model. The model may itself be outdated by today’s standard but the concepts of sensitive variables, critical features and fairness metrics are still relevant today. I would argue they are more than critical even since AI models will soon be deployed in decision making systems that will have a large impact on real people’s lives.